本ページはプロモーションが含まれている場合があります

「正確に円弧をトレースするためのTips - DTP Transit」を読んでいて、正直何をしているのか意味がわかりませんでした(苦笑)。作業自体はできるのですが、なぜそれで円弧から円の中心が出てくるのか…?と訳がわかりませんとツイートしたら、親切なTwitterのフォロワーさん(@rikuo)が答えてくれたよ!
(おそらく正円の)円弧の中心点を求めるのであれば、この方法はどうでしょうか? twitpic.com/87xx69 言葉と記号が足りなかったのですが、線分ABと線分DEは垂直に交わっています。
Twitter / @rikuo: @jdash2000 (おそらく正円の)円弧の中心点 ...
でもそれ(TwitPic)を見てもなぜ垂直な線上に円の中心があるのかわからなかったので教えてもらった日はわからなかったのですが、翌日の朝(出社前)にIllustratorで図を書きながら考えたらわかりました。
わかったときは「エウレカ!」(ガリレオ)という感じで嬉しかったです。 なので記事にしてみました。
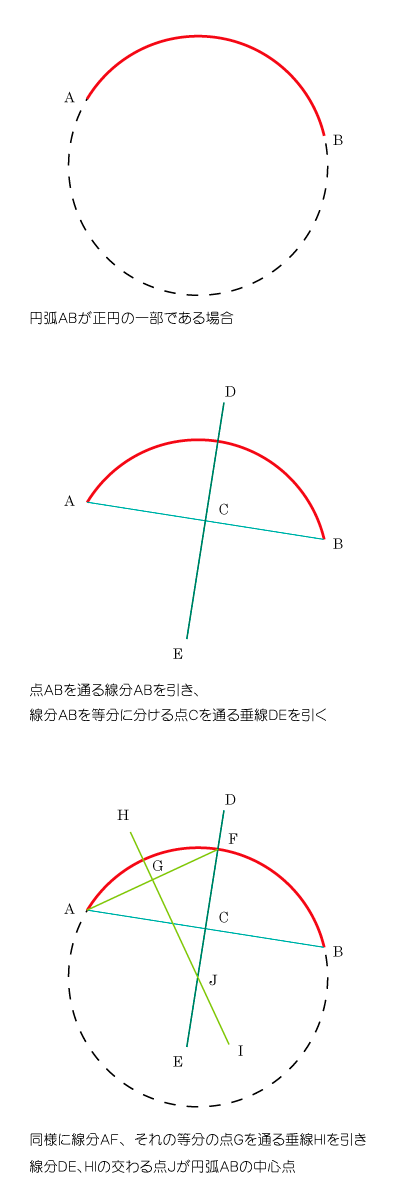
まずは円弧から円の中心が割り出せるのか確認してみる
Illustratorで書いてみます。
まず正丸を書きます。
本当は円弧を書く必要があるのですが、わかりやすく円にしておきます。
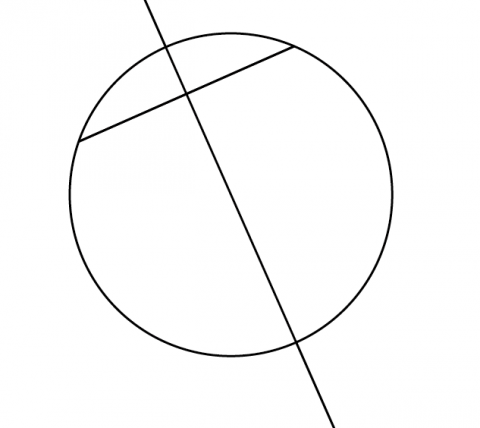
次に直線ツールを使います。
メニューから「表示」→「スマートガイド」にチェックを付けておくと、ポイントがパスに吸着するので正確な作業ができます。
以下の様に円のパス上に2点選択して直線を引きます。

直線パスを直角(90°)に回転します。
回転ツールを使います。

角度に「90°」と入力して、「コピー」をクリックします。
回転させた直線パスの長さが微妙なので(=足りないので)伸ばします。
拡大・縮小ツールを使います。
![]()
今回は400%にしてみました。
以下の様になります。
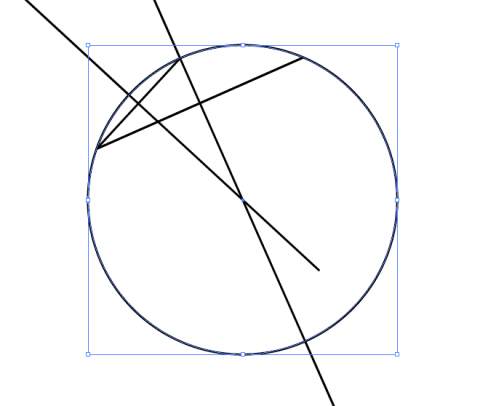
同じようにポイントを2点決定して直線パスを作成します。
今回は検証用に片方のポイントを同じにします。
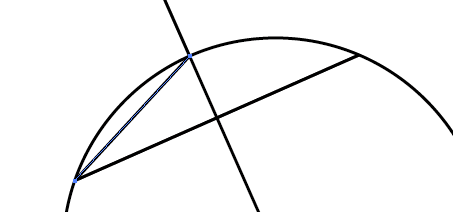
先ほどと同じように、直線パスの回転&コピーと拡大を行っておきます。
直角に回転したパスの交わるところが円の中心になっているはずです。
本当でしょうか?
選択ツールで円を選択します。
![]()
きちんと円の中心と直線パスの交差しているところが円の中心だとわかりますね。
さてここからが本題です。
なぜ直線パスが交差しているところが円の中心になるのか?
補助線を引いてみるとわかりやすいです。
数学の基本ですね(といってもこれに気が付くまでに時間が掛かった…)。
今回は既に円の中心がわかっているので、答えから逆に攻めてみます。答えを証明するといった感じでしょうか。
円の中心から先ほど直線パスを作成するときに選んだポイントへ補助線を引いてみます。
水色・緑色・赤色で引いてみました。
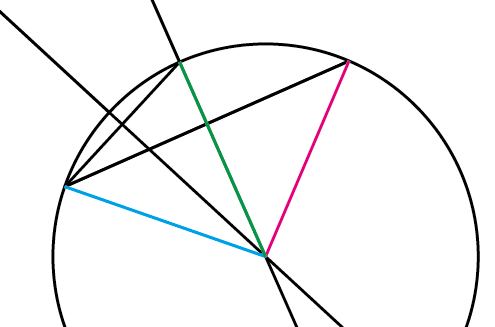
当たり前なのですが、円の中心から円周(つまり円のパス)までは同じ距離です。
つまり、水色・緑色・赤色のパスの長さは同じです。
このため以下の黄色で塗りつぶした図形は二等辺三角形といえます。
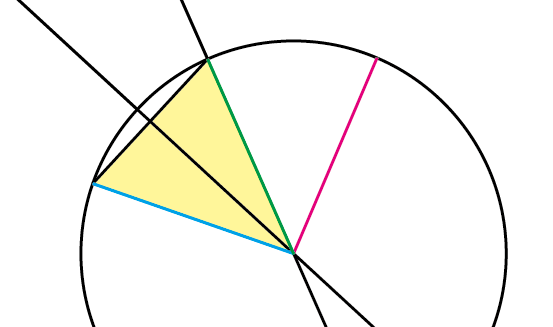
二等辺三角形は、同じ長さの辺以外の辺の中心から、垂直にパスを引くと二等辺三角形の角と交差します。
Illustrator使い的な発想でいえば、以下の黄色に塗られた図形を、緑色のパスの方向にリフレクトツールで反転して配置すれば二等辺三角形ができることがわかります。
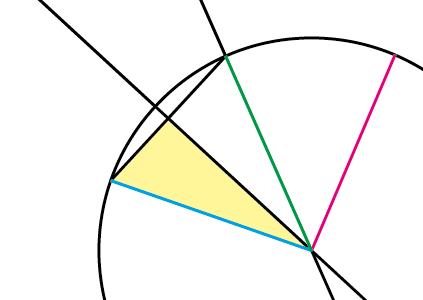
もう一つの水色と赤色のパスの方の二等辺三角形でも同じ事がいえます。
この場合、同じ長さの辺以外の辺の中心から垂直に伸ばすパスが緑色のパスになります。
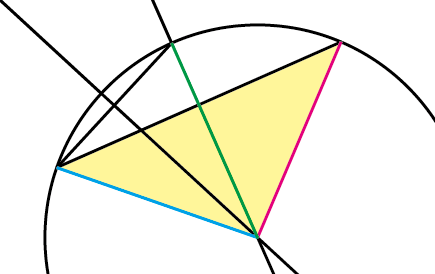
よって、この2つの二等辺三角形の頂点がある位置が円の中心ということになります。
(他に同じように二等辺三角形を作っても頂点が円の中心になる)
確認おわり。
わかると意外とあっさり。Twitterでこんなのは中学生の数学レベルだと誰かが書いていましたが、わかってしまえば確かにそうかもしれません(苦笑)。
余談
本当に「正確に円弧をトレースするためのTips - DTP Transit」の作業が意味がわからなかったので、その記事を見たときは、そんな面倒なことをしなくても「車車車く本牛勿 -Rollin' Real-: Photoshop:マル投げ」「s.h's page - [Illustrator] JavaScript scripts 外接円を描く」で良いだろ!と思いました(笑)。
でも、これらのスクリプトがなぜ三角形を描く(=3つのポイントを設定する)と、円が描けるのか理由がわかりませんでした。
今ならわかります。考えた結果があった! よかった。
今回、このような事を考えるきっかけを与えてくれた「正確に円弧をトレースするためのTips - DTP Transit」に感謝します。 でも未だに何をやっているのかわかりません(苦笑)。
2つの円の中心から同じ距離のポイントで垂直な線を引くってこれはコンパスだよな…って、2点繋ぐと…ああ…わかった様な…(ぼんやりと)。
関連情報・参考資料
- 正確に円弧をトレースするためのTips(DTP Transit)